SCAU 概率论 期末复习（开卷）

news/2025/2/8 20:55:58

说明：由于考试是上机开卷，所以下面写出了求值的代码（java），考试的时候可以直接输入数据即可获得答案。

第四章

1.求下四分位，中位数和上四分位

package com.company;

import java.util.Arrays;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        int n;
        Scanner cin = new Scanner(System.in);
        System.out.println("输入一共有几个数字");
        n = cin.nextInt();


        double[] arr = new double[n];

        System.out.println("输入数组");
        for(int i=0;i<n;i++){
            arr[i] = cin.nextDouble();
        }
        System.out.println("下四分位，中位数，上四分位分别是：");
        System.out.println(Arrays.toString(getQuartiles(arr)));
	// write your code here
    }

    /**
     * 四分位算法
     　　　*@param arr 长度为n的数组
     　　　*@return quartiles Q1/Q2/Q3数组
     **/
    public static double[] getQuartiles(double[] arr) {
        double[] arr1 = new double[4];
        // 长度小于4时,补齐arr数组至长度四位
        if (arr.length < 4) {
            for (int i = 0; i < arr.length; i++) {
                arr1[i] = arr[i];
            }
            for (int k = arr.length; k < 4; k++) {
                arr1[k] = arr1[k];
            }
            return arr1;
        }
        double[] tempArr = Arrays.copyOf(arr, arr.length);
        Arrays.sort(tempArr);
        double[] quartiles = new double[3];

        int n = arr.length;
        double Q1 = (n+1) * 0.25D;
        double Q2 = (n+1) * 0.5D;
        double Q3 = (n+1) * 0.75D;
        //Q1
        if(Q1 % 2 == 0){
            quartiles[0] = tempArr[(int)Q1];
        }else{
            double Q1y = Q1-Math.floor(Q1);
            double Q1r;
            Q1r = (1D - Q1y) * tempArr[(int) Math.floor(Q1)-1] + Q1y * tempArr[(int) Math.ceil(Q1)-1];
            quartiles[0] = Q1r;
        }
        //Q2
        if(Q2 % 2 == 0){
            quartiles[1] = tempArr[(int)Q2];
        }else{
            double Q2y = Q2-Math.floor(Q2);
            double Q2r;
            Q2r = (1D - Q2y) * tempArr[(int) Math.floor(Q2)-1] + Q2y * tempArr[(int) Math.ceil(Q2)-1];
            quartiles[1] = Q2r;
        }
        //Q3
        if(Q3 % 2 == 0){
            quartiles[2] = tempArr[(int)Q3];
        }else{
            double Q3y = Q3-Math.floor(Q3);
            double Q3r;
            Q3r = (1D - Q3y) * tempArr[(int) Math.floor(Q3)-1] + Q3y * tempArr[(int) Math.ceil(Q3)-1];
            quartiles[2] = Q3r;
        }
        return quartiles;
    }
}

2.切比雪夫不等式
任意一个数据集中，位于其平均数m个标准差范围内的比例（或部分）总是至少为1－1/m2，其中m为大于1的任意正数。对于m=2，m=3和m=5有如下结果：
所有数据中，至少有3/4（或75%）的数据位于平均数2个标准差范围内。
所有数据中，至少有8/9（或88.9%）的数据位于平均数3个标准差范围内。
所有数据中，至少有24/25（或96%)的数据位于平均数5个标准差范围内 [2] 。

3.求平均值、总和、标准差、方差

package com.company;

import java.text.DecimalFormat;
import java.util.*;


public class Main{

    public static void main(String[] args) {
        int n;
        Scanner cin = new Scanner(System.in);
        System.out.println("输入数字的个数：");
        n = cin.nextInt();
        double[] x = new double[n];
        for (int i = 0; i < n; i++) {// 随机生成n个double数
            x[i] = cin.nextDouble();
        }
        // 设置doubl字符串输出格式，不以科学计数法输出
        DecimalFormat df = new DecimalFormat("#,##0.00");// 格式化设置
        // 计算方差
        double dV = Variance(x);
        System.out.println("方差=" + df.format(dV));
        // 计算标准差
        double dS = StandardDiviation(x);
        System.out.println("标准差=" + df.format(dS));

    }

    //方差s^2=[(x1-x)^2 +...(xn-x)^2]/n 或者s^2=[(x1-x)^2 +...(xn-x)^2]/(n-1)
    public static double Variance(double[] x) {
        int m=x.length;
        double sum=0;
        for(int i=0;i<m;i++){//求和
            sum+=x[i];
        }
        System.out.println("总和="+sum);
        double dAve=sum/m;//求平均值
        System.out.println("平均值="+dAve);
        double dVar=0;
        for(int i=0;i<m;i++){//求方差
            dVar+=(x[i]-dAve)*(x[i]-dAve);
        }
        return dVar/m;
    }

    //标准差σ=sqrt(s^2)
    public static double StandardDiviation(double[] x) {
        int m=x.length;
        double sum=0;
        for(int i=0;i<m;i++){//求和
            sum+=x[i];
        }
        double dAve=sum/m;//求平均值
        double dVar=0;
        for(int i=0;i<m;i++){//求方差
            dVar+=(x[i]-dAve)*(x[i]-dAve);
        }
        //reture Math.sqrt(dVar/(m-1));
        return Math.sqrt(dVar/m);
    }
}

4.知道标准差和平均值，求某范围占比
利用正态分布来计算
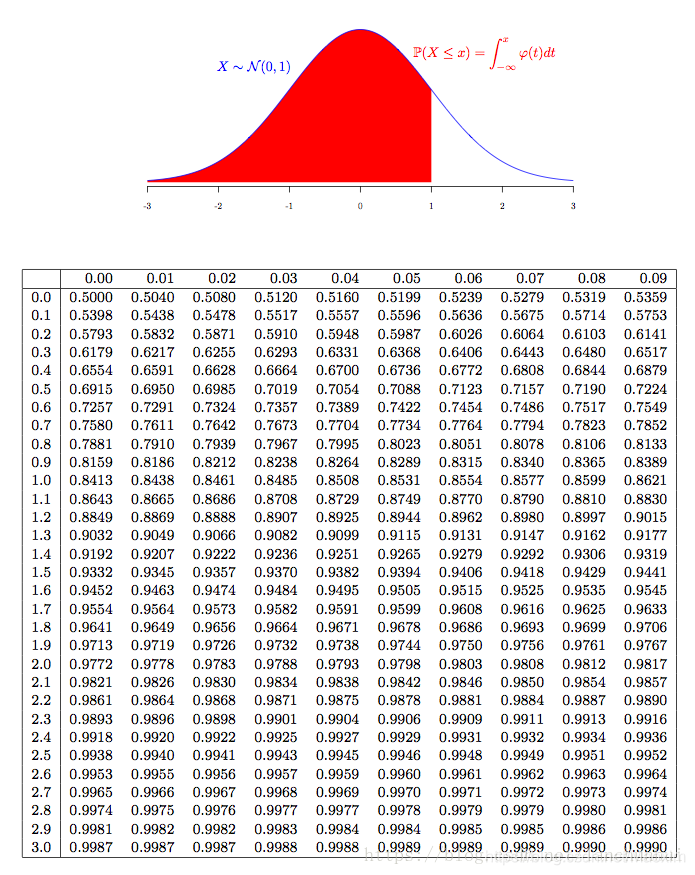
在这里插入图片描述
5.离散系数
一组数据的标准差与其相应的均值之比，是测度数据离散程度的相对指标，其作用主要是用于比较不同组别数据的离散程度。 其计算公式为
在这里插入图片描述

在对比情况下，离散系数较大的其分布情况差异也大。

6.计算峰态系数

package com.company;

import java.util.Scanner;

public class Main{

    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int t;
        System.out.println("输入总共数字个数：");
        t =cin.nextInt();
        int n;
        System.out.println("输入不同数的个数：");
        n = cin.nextInt();
        double[] a =new double[n];
        System.out.println("输入数组");
        for(int i=0;i<n;i++){
            a[i] = cin.nextDouble();
        }
        int[] b = new int[n];
        System.out.println("分别输入每个数的频数：");
        for(int i=0;i<n;i++){
            b[i] = cin.nextInt();
        }
        System.out.println("输入标准差：");
        double s;
        s = cin.nextDouble();
        double x =0;
        for(int i=0;i<n;i++){
            x+=a[i]*b[i];
        }
        x/=t;

        double r1 =0;
        for (int i=0;i<n;i++){
            r1 += (a[i]-x)*(a[i]-x)*(a[i]-x)*(a[i]-x)*b[i];
        }
        double result;
        result = r1/(t*s*s*s*s)-3;
        System.out.println("峰态系数"+result);
        if(result>0){
            System.out.println("尖峰分布");
        }
        else if(result<0){
            System.out.println("平峰分布");
        }
        else {
            System.out.println("标准分布");
        }



    }
}

第五章

1.求带概率的标准差
先算期望 E(X) = 10.25 + 20.45 + 3 0.3 = 2.05再算 E(X²) = 1²0.25 + 2²*0.45 + 3² *0.3 = 4.75所以方差D(X)=E(X²)-E(X)²=0.5475标准差就开根号 为 0.74

第七章

1.求置信区间

package com.company;

import java.util.Scanner;

public class Main{

    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int n;
        System.out.println("输入样本的数量：");
        n = cin.nextInt();
        double x;
        System.out.println("输入样本的均值：");
        x = cin.nextDouble();
        double variance;
        System.out.println("输入方差，或者标准差的平方：");
        variance = cin.nextDouble();
        System.out.println("输入概率的正态值(95%的值是1.96)：");
        double y;
        y = cin.nextDouble();
        double v = Math.sqrt(variance) / Math.sqrt(n);
        System.out.println(x+"-"+y*v +","+x+"+"+ y*v);
        System.out.println(x- y*v +","+(x+ y*v));

    }
}

补充（方便运算）

次方运算

package com.company;

import java.util.Scanner;

public class Main{

    public static void main(String[] args) {
        System.out.println("请输入几的几方：");
        double a;
        int n;
        double result=1;
        Scanner cin = new Scanner(System.in);
        a = cin.nextDouble();
        n = cin.nextInt();
        for(int i=0;i<n;i++){
            result = result*a;
        }
        System.out.println("结果是:"+result);

    }
}

2.显著性水平
在这里插入图片描述

package com.company;

import java.util.Scanner;

public class Main{

    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        System.out.println("输入标准差：");
        double deviation;
        deviation = cin.nextDouble();
        System.out.println("输入取了多少个样品n：");
        int n;
        n = cin.nextInt();
        System.out.println("输入x的均值：");
        double x;
        x = cin.nextDouble();
        System.out.println("输入平常的值u：");
        double u;
        u = cin.nextDouble();
        System.out.println("显著水平的值(0.05则输入1.96)；");
        double v;
        v = cin.nextDouble();

        double result;
        result = (x-u)/(deviation/Math.sqrt(n));
        if(result>=v||result<=-v){
            System.out.println("result:"+result);
            System.out.println("则有显著的比变化");
        }
        else {
            System.out.println("result:"+result);
            System.out.println("没有有显著的比变化");

        }
        System.out.println(result);
    }
}

标准正态分布的一些常用的概率的值是90%,95%,98%,99%:
1.28 0.8997
1.65 0.9505
1.96 0.9750
2.06 0.9803
2.33 0.9901


http://www.niftyadmin.cn/n/4058284.html

相关文章

远程访问大华摄像头_通过WEB调用大华网络摄像头

远程访问大华摄像头_通过WEB调用大华网络摄像头

通过WEB调用大华网络摄像头1.要调用的大华摄像头为Dahua 大华DH-IPC-HFW2100P-0600B 网络摄像机 (白色)&#xff0c;摄像头外形如下图所示2.调用效果如下图所示4.解压OCX包单击文件中的reg.bat注册dll5.新建index.html关输入以下代码视频控件body {font-family:"", a…
阅读更多...
面试题14：剪绳子（动态规划，贪心算法）

面试题14：剪绳子（动态规划，贪心算法）

一、题目&#xff1a; 一根长度为n的绳子&#xff0c;剪成m段,m,n都大于1&#xff0c;且都为整数,每段长度记为k[0],k[1]…,k[m].求k[0]*k[1]…*k[m]可能的最大乘积 1.1解法&#xff1a; 两种不同的方法解决这个问题&#xff0c;先用常规的需要O(n)时间和O(n)空间的动态规划…
阅读更多...
python re模块导入_Python正则re模块使用步骤及原理解析

python re模块导入_Python正则re模块使用步骤及原理解析

python中使用正则表达式的步骤&#xff1a;1.导入re模块&#xff1a;import re2.初始化一个Regex对象&#xff1a;re.compile()3.刚刚创建的Regex对象调用search方法进行匹配&#xff0c;返回要给March对象4.刚刚的March对象调用group方法&#xff0c;展示匹配到的字符串下面例…
阅读更多...
面试题4：二维数组的查找

面试题4：二维数组的查找

一、题目 在一个二维数组中&#xff0c;每一行都按照从左到右递增的顺序排序。每一列都按照从上到下递增的顺序排序&#xff0c;请完成一个函数&#xff0c;输入这样的一个二维数组和一个整数&#xff0c;判断数组是否含有该整数。 二、算法分析 一个从左到右&#xff0c;从…
阅读更多...
6脉冲触发器脉冲缺失_脉冲袋式除尘器6个主要构件特点及5个常见问题及处理措施...

6脉冲触发器脉冲缺失_脉冲袋式除尘器6个主要构件特点及5个常见问题及处理措施...

随着国家环保要求越来越高&#xff0c;对大气粉尘污染的严格管控&#xff0c;除尘设备在多领域得到大量应用&#xff0c;在防治粉尘污染、改善作业环境、实现烟气达标排放方面发挥着很大作用。本文分享脉冲袋式除尘器6个主要构件特点及5个常见问题及处理措施。1.脉冲袋式除尘器…
阅读更多...
快速排序及五种优化（模板）

快速排序及五种优化（模板）

1、快速排序的基本思想&#xff1a; 快速排序排序使用分治的思想&#xff0c;通过一趟排序将待排序列分割成两部分&#xff0c;其中一部分记录的关键字均比另一部分记录的关键字小。之后分别对这两部分记录继续进行排序&#xff0c;递归地以达到整个序列有序的目 2、快速排序…
阅读更多...
SCAU 汇编语言 期末复习 (上）

SCAU 汇编语言 期末复习 (上）

第一章 1.储存单位 存储容量&#xff1a;bit 、Byte、 Word 1 kilobytes210bytes1024bytes 1megabyte(MB)220bytes 1gigabyte(GB)230bytes 1terabyte(TB)240bytes 1petabyte250bytes 1exabyte260bytes 1zettabyte270bytes 1yottabyte280bytes 2个字节&#xff1a; Word &#…
阅读更多...
双光耦开关电源电路图_六款简单的开关电源电路设计原理图详解

双光耦开关电源电路图_六款简单的开关电源电路设计原理图详解

简单的开关电源电路图(一) 简单实用的开关电源电路图调整C3和R5使振荡频率在30KHz-45KHz。输出电压需要稳压。输出电流可以达到500mA.有效功率8W、效率87%。其他没有要求就可以正常工作。简单的开关电源电路图(二)24V开关电源&#xff0c;是高频逆变开关电源中的一个种类。通过…
阅读更多...
最新文章

Copyright @ 2022~2023